ARTS-Week9

Algorithm

Problem

[33.] Search in Rotated Sorted Array

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm’s runtime complexity must be in the order of O(log n).

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Thought

This problem is almost the same to binary-search which can be solved in O(log n), except that the input array is partly-sorted.

In order to solve it with O(log n) complexity, we must reduce array count by half every iteration. This is the keypoint.

Solution

This solution comes from this clever idea, and it’s quite a gennius solution.

For a fully sorted array in ascending order, if target is greater than middle, thus search again in the upper half, otherwise the lower half.

But it’s not actual for a rotated array in this problem, unless importing some tricks.

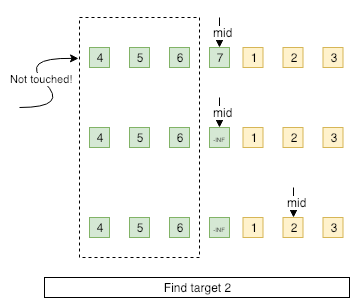
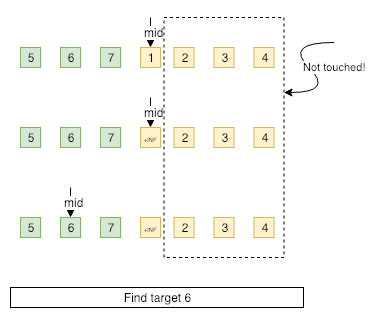
Rotating at a pivot divides the initial sorted array to two parts. Both parts are still in ascending order, and what’s more, element of first part is greater than anyone of the second part.

We can compare the middle and target to check if they are at the same part. If they are in either part, we can then search in this part directly, and the following search becomes a normal binary-search problem.

But what if the middle and the target are at the opposite part? If it happens, we must modify the middle value to -INIFITY or +INIFITY according to the part the middle embeddes in, pretending that the array is a fully sorted array. Afterwards, the binary-search should proceed.

Following two simple examples demonstrate the gennius thought.

And see the codes:

class Solution {
public:
int search(vector<int>& nums, int target) {
    int lo = 0, hi = nums.size();
    while (lo < hi) {
        int mid = (lo + hi) / 2;
        
        double num = (nums[mid] < nums[0]) == (target < nums[0])
                   ? nums[mid]
                   : target < nums[0] ? -INFINITY : INFINITY;
                   
        if (num < target)
            lo = mid + 1;
        else if (num > target)
            hi = mid;
        else
            return mid;
    }
    return -1;
}
};

Review

Secret sharing scheme

Tip

Whenever a segmentation fault occurres, please keep calm.

Reference-1 shows you easy steps to debug a segfault.

In conclusion:

1. ulimit -c unlimited
2. sysctl -w kernel.core_pattern=/tmp/core-%e.%p.%h.%t
3. gdb [binary-file] [core-dump-file]

Share

How to Be A Programmer

As the author says, to be a good programmer is difficult and noble. Writing programs is important indeed and brain burning, but easier when compared to other things such as cooperating with both customers and colleagues.

He present some efficient ways to be a good programmer in many different dimensions, including personal skills, team skills and etc.

It’s worthy to read although it was written in 2002.

Section [3.2] How To Recognize When To Break or Go Home tells you to balance with life and work, and it’s really really important. When you are stuck in some hard problem, just walk away and take a cup of coffee, and you probably will find new possible solution.

Section [3.5] How to Document Wisely presents the importance about writing good documentation. Documentation, like testing, can take many times longer than developing code, but it deserves.

Section [9.8] How to Tell People Things They Don’t Want to Hear shows you how to tell hard things to stakeholders. The best way to tell someone about a problem is to offer a solution at the same time. If none possible solution exists, such as when schedule slip occurres, keep stakeholders informed at the first time no matter how hard you may think of it.

Many many intelligent thoughts in it, and hope you will like it.

Reference

1. Debugging a segfault on linux